Anmerkung zur Version Die vorliegende Version des Artikels wurde am 02.11.2012 geringfügig formal korrigiert.
- Einleitung
- Diagramme als Erkenntnismittel
- Das Diagramm bei Peirce
- Exkurs zu den Existential Graphs
- Diagrammatik in der Informationswissenschaft
Einleitung
Die Formen des „Sichtbarmachens“ in der Wissenschaft reichen von „Abbildungen“ über „Modelle“ bis hin zu „Simulationen“. Sie können u.a. gezeichnet, fotografiert, geometrisch konstruiert oder durch Sensorik vermittelt, digital prozessiert werden. Ihre Funktionen erstrecken sich von der Orientierung bis hin zur (hypothetischen) Voraussage und somit auch vom Überblick bis zur Evidenzsuggestion. Generell handelt es sich um vereinfachte (und vereinfachende) Darstellungen von (teilweise sehr komplexen) Sachverhalten, zu deren Verständnis sie beitragen sollen; daher können sie bei Lernprozessen, d.h. in der Vermittlung und auch bei der Organisation von Wissen eine wichtige Rolle spielen. Diese kommt ihnen nun nicht nur zu, weil sie – wie in den mittelalterlichen Mnemotechniken – als Gedächtnisstützen für bekannte Sachverhalte dienen. Sondern resultiert auch aus ihrem Potenzial für die Entdeckung von neuen Zusammenhängen. Der folgende Artikel diskutiert die Darstellungsform des Diagramms. Es wird hier mit dem Gedanken gespielt, dass die in der universalen Zeichentheorie von C.S. Peirce entwickelte Diagrammatik wichtige Impulse für eine Untersuchung des Zusammenhangs von Wissen und Bildlichkeit geben kann.
Diagramme als Erkenntnismittel
Und auf welche Weise willst du denn dasjenige suchen, Sokrates, von dem du überhaupt nicht weißt, was es ist. [Fn 01]
Eine berühmte und oft zitierte Stelle in Platons Dialog Menon ist der sogenannten „Paradoxie des Lernens“ [Fn 02] gewidmet: Wie können wir mit unserem derzeitigen Wissen zu neuen Einsichten gelangen, wenn die Möglichkeit dazu auf diesen Wissenstand selbst beschränkt ist? Sokrates, der sich nicht mit diesem Paradox zufrieden geben will, löst das Problem mit dem Hinweis auf die anamnesis. Die „Wiedererinnerung“ an ewige Ideen sei es, die es uns ermögliche in dieser Situation doch noch zu einem Ergebnis zu gelangen: Wir wissen etwas, von dem wir nicht wissen, dass wir es wissen und an dieses Wissen können wir uns „erinnern“. Dies demonstriert Sokrates durch die Befragung eines Sklavenjungen, in deren Verlauf er geometrische Figuren aufzeichnet. Mit deren Hilfe wird es dem Knaben möglich, die Frage nach der Seitenlänge eines Quadrates, das von doppelter Größe als das vorgegebene sein soll, zu lösen. Sokrates beweist hier zwar – seine Rolle als kundiger Befrager ausblendend – die Möglichkeit des Lernens. Seinem Hinweis auf die (scheinbar „eingeborenen“ und der „Wiedererinnerung“ zugänglichen) Ideen der unsterblichen Seele mag man jedoch heute vielleicht nicht mehr so gern folgen. Außerdem: Wer genau hinschaut, kann feststellen, dass die geometrischen Diagramme im hier demonstrierten Lernprozess die Einsicht überhaupt erst möglich machen, diese also nicht nur einem „internen“ Wissen des Einzelnen entspringt. Um das Verhältnis von Wissen und seiner Visualisierung im Lernen und Schlussfolgern zu verstehen wird sich der Blick daher auf die Rolle der geometrischen Diagramme richten müssen. [Fn 03]
Diese Problemstellung ist in vielen Aufsätzen und Manuskripten von Charles Sanders Peirce (1839-1914) zentral. Wobei Peirce eine zu Platon genau entgegengesetzte Position einnimmt: Für ihn ist das Verhältnis von Darstellung/Zeichen und Erkenntnis wesentlich. Im Zentrum seiner Überlegungen steht daher das diagrammatic reasoning, von dessen Ubiquität er überzeugt war und ihn dazu bewog eine bildliche Graphenlogik zu entwickeln. Für Peirce ist überhaupt alles Denken, im gültigen Sinne aber insbesondere das notwendige Schlussfolgern „diagrammatisch“. [Fn 04] Denn das Problem der Zeichen und das Problem der Logik fallen für ihn zusammen. Es würde hier zu weit führen seinen Ansatz ausführlich zu skizzieren. An dieser Stelle ist entscheidend, dass Peirce, anknüpfend an Kants Schematismusproblem, sich besonders intensiv mit dem Problem der Bildlichkeit der Logik auseinandergesetzt hat. [Fn 05]
Das Diagramm bei Peirce
Der Gedanke, dass ein Diagramm mehr als ein unwesentliches Hilfsmittel sein könnte, zeichnet sich bereits bei Kant ab. Was Kant bei seiner Untersuchung der Bedingungen der Möglichkeit von Erkenntnis auffiel und er auch den „Schematismus der reinen Verstandesbegriffe“ nannte, ist die Synthese von „Verstand“ (Begriff) und „Sinnlichkeit“ (Anschauung) in der Erkenntnis. [Fn 06] Dies zeigten ihm insbesondere geometrische Beispiele. [Fn 07] Somit rückt nun auch das Erkenntnismittel (und das Medium) in den Fokus. An diesen Gedanken schließt Peirce mit seinem Begriff des diagrammatic reasoning an. Dem triadischen Zeichenbegriff der semeiotic, [Fn 08] bestehend aus der Relation von „Objekt“ (O), „Zeichen“ oder „Zeichenträger“ (vehicle, Z) und „Interpretant“ (I), liegt dabei die Idee zu Grunde, dass es Zeichen nur in Aktion, also als dynamische Phänomene, geben kann. So kann sowohl das Repräsentationsverhältnis von „Objekt“ und „Zeichenträger“ (O/Z), wie auch das Wirk- oder Interpretationsverhältnis von „Zeichenträger“ und „Interpretant“ (Z/I) unter einen Begriff gebracht werden. Diese dynamische Konzeption wirkt sich auf das Verständnis der spezielleren Zeichenarten aus, die Peirce unterschieden hat, so auch auf das Diagramm, das für ihn eine Unterkategorie des Ikonischen bildet. Das Ikon ist eine der drei Formen, die Peirce im Objektbezug (O/Z) unterscheidet; die anderen beiden sind bekanntlich Index und Symbol. [Fn 09] Während ein Index in einer direkten (reaktiv-kausalen) Relation zum Objekt steht und das Symbol durch Konventionalität (Regel, Gewohnheit) geprägt ist, funktioniert das Ikon durch die Ähnlichkeit zum Objekt – oder wie Peirce auch sagt, durch geteilte Charakteristika. [Fn 10] Ähnlichkeit scheint zunächst ein sehr vages Kriterium zu sein und wurde in der Semiotik oft als problematisch angesehen, da es ein zu subjektives, psychologistisches Prinzip der Identifizierung suggeriert. Auch Peirce schwankte, was die Ähnlichkeitsdefinition anging. Daher wurde später das gesamte Konzept der Ikonizität entweder ignoriert oder als unbrauchbar abgetan. In seiner großangelegten Studie Diagrammatology (2007) weist Frederik Stjernfelt diese Interpretation der Ikonizität zurück: Ähnlichkeit definiere sich bei Peirce nicht durch Identität, sondern als Kriterium für die Ikonizität vor allem über seine Operationalität. [Fn 11] In der Tat schreibt Peirce in einem Text von 1895:
For a great distinguishing property of the icon is that by the direct observation of it other truths concerning its object can be discovered than those which suffice to determine its construction. [Fn 12]
Hier wird deutlich, wie sich für Peirce die Repräsentation bestimmter Qualitäten (O/Z) mit der Funktion im Interpretationsprozess (Z/I) verbindet. Die Zeichenform des Ikonischen unterteilt Peirce dann ebenfalls noch einmal triadisch:
Icons may be distinguished, though only roughly, into those which [represent] are icons in respect to qualities of sense, being images, and those which are icons in respect to the dyadic relations of their parts to one another, being diagrams or dyadic analogues, and those which are icons in respect to their intellectual characters, being examples. [Fn 13]
Das Diagramm stellt bei Peirce also eine bestimmte Form des ikonischen Zeichens dar. Es wird als eine Darstellung von „intellektuellen Relationen“ definiert, die im Unterschied zu anderen ikonischen Formen bestimmten Regeln unterliegt. Hier wird der besondere Vorzug von Diagrammen deutlich, der in der Verbindung von bildlichen und arbiträren, (in Peirces Diktion also) von ikonischen und symbolischen Elementen besteht. [Fn 14] Diagramme zeigen, indem sie ihre Eigenschaften, die strukturähnlich zum angenommen Sachverhalt konstruiert werden, bildlich ausstellen, denn ein Ikon drückt seine Verbindung zum Objekt immer auch durch seine interne Organisation aus. [Fn 15] Nach Peirces Ansicht erfüllt das Diagramm damit eine grundlegende Aufgabe, denn ihm entspricht hier die abduktive Schlussform der Hypothesenbildung: der einzigen Schlussform durch die etwas Neues in den Schlussprozess eingeführt werden kann. [Fn 16] Es ist dementsprechend nach Peirce möglich durch Interpretation, Manipulation und „Beobachtung“ eines Diagramms mehr zu Lernen, als an Wissen in seine Konstruktion eingeflossen ist. Wie funktioniert das?
Im Umgang mit Diagrammen können Konstruktion/Interpretation und Manipulation/Beobachtung hintereinander geschaltet werden. Zunächst wird dabei eine Hypothese in das topologische Skelett eines möglichen Sachverhaltes überführt. Ein wichtiger Effekt dieser Diagrammatisierung ist, dass durch die Darstellung Vor- und Hintergrundannahmen – was Peirce collateral knowledge [Fn 17] nannte – anschaulich gemacht werden. So wird es möglich, auf diese explizit gemachten Vorannahmen dann selbst wiederum zu reflektieren. [Fn 18] Das geschieht z.B. durch (zweidimensionale) Verräumlichung in der Konstruktion. So in der Fläche angeordnet können neue Aspekte eines Sachverhalts entdeckt werden, was insbesondere bei topologischen Verhältnissen offensichtlich ist. Außerdem kann an Diagrammen „experimentiert“ werden. Im Prozess des diagrammatischen Experimentierens lässt sich das Diagramm (z.B. durch Einführung neuer Elemente) manipulieren, wobei die Manipulation bestimmten Anwendungsregeln unterliegen kann. Das macht, wie angedeutet, die semiotische Hybridform des Diagramms aus und war für Peirce der Ansatzpunkt für die Entwicklung einer graphischen Logik.
Es ist interessant, dass jemand wie Peirce, der an der Weiterentwicklung der symbolischen Logik (algebra of logic) entscheidenden Anteil hatte, sich später ganz der Ausarbeitung eines logischen Graphensystems widmete. Das sollte nicht als Idiosynkrasie, sondern als Versuch angesehen werden, ein diagrammatisches System zu entwickeln, das die Vorteile von „ikonischen“ und „symbolischen“ Logiken vereinen kann. [Fn 19] Hier sei zunächst darauf hingewiesen, dass neben der von Stjernfelt betonten operationalen „non-trivial icon definition“, [Fn 20] die letztlich durch das Kriterium der Neuheit keinen Unterschied zwischen unterschiedlichen (O/Z)-Relationsformen macht, noch ein weiterer Aspekt der Ikonizität eine Rolle spielt. Bei der Entwicklung des logischen Systems der Existential Graphs (EG) ging es Peirce nämlich auch um eine optimale Ikonizität für die logischen Graphen. [Fn 21]
A diagram ought to be as iconic as possible, that is, it should represent relations by visible relations analogous to them. [Fn 22]
Das Kriterium „ikonisch“ impliziert hier eine realistische Auffassung. Denn im Falle der Äquivalenz zweier Systeme sei dasjenige vorzuziehen, dass die Strukturähnlichkeit am besten zum Ausdruck bringt. [Fn 23] Dies geschieht im Sinne der Einfachheit und Effektivität des Systems. Für Peirce ist das der entscheidende Grund, auch in der Logik diagrammatische Systeme zu bevorzugen. Anders gezeigt: Es macht offensichtlich einen Unterschied, ob man versucht die (O/Z/I)-Relation im unendlichen Zeichenprozess (semiosis) zu beschreiben oder graphisch darstellt:
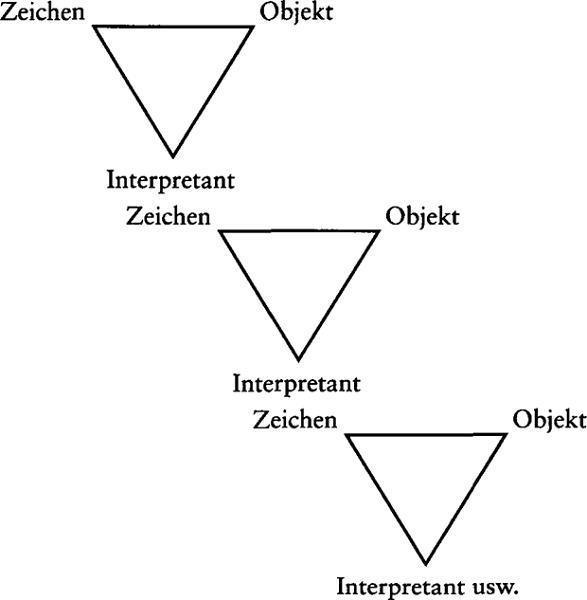
Abbildung 1: Semiose
Dementsprechend führt Peirce am Beispiel der Existential Graphs (EG) aus:
[The] purpose of the System of Existential Graphs […is] to afford a method (1) as simple as possible (that is to say, with as small a number of arbitrary conventions as possible), for representing propositions (2) as iconically, or diagrammatically and (3) as analytically as possible. [Fn 24]
Diese drei Kriterien bezeichnet er als die „three essential aims of the system“ [Fn 25] logischer Graphen. Hervorzuheben ist dabei der Versuch Einfachheit und Präzision zu verbinden.
Die neueren Forschungen der Logikerin Sun-Joo Shin schließen hier an, um die Relevanz diagrammatischer Systeme im Feld der formalen Logiken aufzeigen. Shin meint, dass “[t]he dominance of sentential representation systems in the history of modern logic has obscured several important facts about diagrammatic systems.” [Fn 26] Die EG sind für sie Beispiel eines „Efficient, Formal, Representation System for Logic”, [Fn 27] d.h. eines Systems, das eine sowohl formal akkurate, wie auch semiotisch effiziente Formalisierungsform bilden kann. Das zeige, dass das enge Verständnis eines formalen Systems zu hinterfragen ist, die Möglichkeiten der Formalisierung zu erweitern sind und nicht nur auf symbolisch-linguistische Logiksysteme beschränkt bleiben müssen. Die Alternative von logischer Konsistenz vs. einfacher Anwendbarkeit (d.h. Effektivität) sieht Shin nicht als zwangsläufige Dichotomie an, da dies auf der Unterscheidung von logischen Systemen und effektiven Kalkülen beruht, die man mit einer modifizierten Lesart der EG oder dem Entwurf eines ähnlichen diagrammatischen Systems vermeiden könne. Ihr Modifizierungsvorschlag bezieht sich u.a. auf die Lesart der Graphen: Um den syntaktischen Einschränkungen zu entgehen, die eine an der symbolischen Logik orientierte sukzessive Lesart (endopeuretic reading) mit sich bringt, seien die Vorteile, die durch die Ikonizität der Graphen entstehen auszunutzen. [Fn 28] So kann die Mehrdeutigkeit von Darstellungen (simultanous plurality) positiv als Möglichkeit multipler Lesarten genutzt werden. Bei der symbolischer Logik [Fn 29] wären multiple Lesarten verheerend, da die Bedeutung einer Formel ambig wird. Für den Graphen dagegen böten sich mehrere, und zwar jeweils klar abgrenzbare, Möglichkeiten an. Multiple Lesarten bedeuten hier, nach Shin, nicht, dass das ganze System wegen Uneindeutigkeit zusammenbricht, sondern dass es vielmehr eine weitaus größere Effizienz erhält. [Fn 30]
Exkurs zu den Existential Graphs
Ausgehend von seinem Konzept der Ikonizität entwickelte Peirce in mehreren Anläufen eine graphische Logik. Das Ergebnis dieser Bemühungen waren die sogenannten Existential Graphs (EG), durch die es gelang „logische und semantische Beziehungen durch das Enthaltensein von Linien und Formen auf einer Fläche“ [Fn 31] darzustellen. Zwei Systeme konnte Peirce beenden (Alpha- und Beta-Graphen), ein weiteres liegt in groben Zügen vor (Gamma-Graphen). [Fn 32] Grundlegend ist folgende Struktur: Alles was auf dem sogenannten Behauptungsblatt (sheet of assertion) steht, welches das Diskursuniversum darstellt, ist eine Aussage. Das ‚weiße Blatt’ bzw. der Hintergrund ist also wesentlicher Teil der Graphen und wenn das Blatt leer bleibt, ist diese Leerstelle selbst ein Graph. Hier das Notationsprinzip:
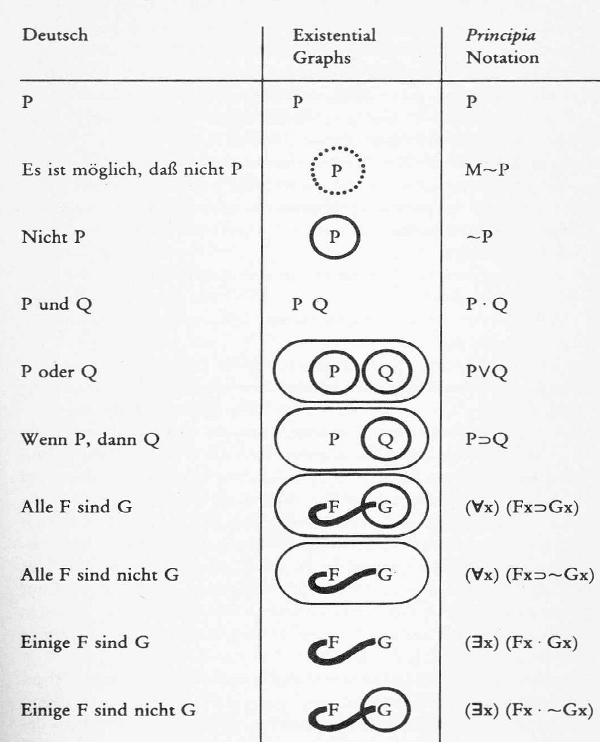
Abbildung 2: Tabelle der graphischen und algebraischen Notationen
Die Identitätslinie (line of identity), mit fettem Federstrich dargestellt („Alle F sind G“), behauptet die Identität der Einzeldinge, welche sie verbindet. Ausschließung (cut) wird mit einer durchgezogenen Linie dargestellt, die alles, was sie umschließt, von dem Behauptungsblatt trennt. Das eingekreiste P in der Abbildung bedeutet also eine Negation von P. Der cut ist nicht so sehr als Linie, als vielmehr als Grenze, eben als „Schnitt” zu lesen. [Fn 33] Frühe Versuche mit der graphischen Logik von Peirce benutzten den s/w Kontrast zur Darstellung von Negation, was Peirce jedoch unpraktikabel fand, da man in diesem Fall ständig mit Tinte ausfüllen musste. Den spielerischen und teilweise bis ins Absurde getriebenen Umgang, den er bei seinen graphischen und zeichnerischen Experimenten pflegte, veranschaulicht folgende Zeichnung von Peirce (Abbildung 3):

Abbildung 3: Zeichnung Peirce
Die nachträglich bearbeitete schwarze Färbung in Abbildung 4 beruht auf dem logischen Prinzip der Negation. So kann man wunderbar das Prinzip des cuts nachvollziehen. Man könnte nun also spekulieren, ob damit das Abgetrenntsein der rechten kleineren Figur vom Hintergrund illustriert ist und die Zeichnung innerhalb der Tabelle die letzte Behauptung darstellt (also im Schema „Einige F sind nicht G“ – da die rechte Person komplett vom Blatt abgetrennt wird, zwischen den beiden Personen trotzdem eine Identitätslinie besteht und die linke Person dennoch nicht komplett umschlossen ist) oder ob hier eine gegenseitige Aufhebung vollzogen wird. Wie man die dargestellte Situation sowie die Rolle der Nasen deuten möchte und noch auf die anderen Figuren ausweiten könnte, bleibt letztlich jedem selbst überlassen.
Lange Zeit blieb Peirces System der EG unbeachtet. Allgemein wurde es als zu kompliziert und beschränkt angesehen. In der Informatik, speziell in der Computerlinguistik und KI-Forschung, wurden die EG jedoch bereits aufgegriffen. Man nutzte das Konzept der EG dort unter der Bezeichnung conceptual graphs unter anderem zur Modellierung von semantischen Netzen , wobei es sich um nahezu das gleiche Logik-Konstrukt handelte, welches lediglich unter einem anderen Namen firmierte: „Conceptual graphs are extensions of existential graphs with new features based on the semantic networks of AI and the linguistic research on thematic roles and generalized quantifiers.“ [Fn 35] Dies macht deutlich, dass sich das Prinzip der EG durchaus praktisch anwenden und zum Bereich der Wissensrepräsentation hin erweitern lässt.
Diagrammatik in der Informationswissenschaft
Aber welche Rolle spielen diagrammatische Darstellungen in der Wissensorganisation? Und wurde das beschriebene ikonische Potenzial von Diagrammen bisher in diesem Kontext genutzt?
In der informationswissenschaftlichen Diskussion, speziell im Bereich der Wissensrepräsentation existieren vereinzelt theoretische Auseinandersetzungen mit diesen Fragen. Einen fruchtbaren Ansatz für das Verständnis von Repräsentationsprozessen scheint die Semiotik zu bieten. [Fn 36] So beschreibt Søren Brier die Tätigkeit des Indexierens mit Bezug auf die Peirceschen Zeichenkategorien. [Fn 37] Alon Friedman und Martin Thellefsen, die angeben, in ihrem Ansatz erstmalig Wissensrepräsentation, Semiotik und Konzepttheorie zu kombinieren, beschränken sich dagegen wiederum ausschließlich auf Sprache als Medium im Zeichenprozess. „The level of signification“ bezieht sich dort auf die Eigenschaften von Sprache, nämlich Syntax, Grammatik, Form, Word und klammert die Bildlichkeit aus.
Es scheint ergiebiger zu sein die Praxis der Wissensorganisation semiotisch zu analysieren. [Fn 38] Die Inhaltserschließung als wesentliche Tätigkeit der Wissensorganisation gibt Aufschluss über das Prinzip der Repräsentation im informationswissenschaftlichen Kontext. Brier zeigt in Cybersemiotics ein Problem der natürlichsprachlichen Basis traditioneller Wissensorganisationssysteme auf. Die verschiedenen Sprachspiele (nach Wittgenstein) des Autors des Dokuments, des Nutzers, der Klassifikation und des Indexierers, welches er als „not so much technical more socio-linguistic“ [Fn 39] verortet. Der Verweisungszusammenhang ist nicht von dem jeweiligen Kontext des Objekts (Fachdisziplin) und der dazugehörigen Sprache (Terminologie) trennbar. Durch den Interpretationsprozess, der von der jeweils eigenen ‚Sprache’ des Indexierers oder Nutzers geprägt ist, werden Missverständnisse wahrscheinlicher. Hinzu kommt, dass das Verhältnis von Dargestelltem und Darstellendem in Bezug auf Sprache von Arbitrarität geprägt ist, zumindest wenn man von der Semiologie Saussures ausgeht.
Beim Prozess des Indexierens im Bereich des information retrieval werden die Repräsentationen von Objekten oder Sachverhalten nach bestimmten Regeln (z.B. Klassifikationen) generiert, um die Objekte zu beschreiben und wiederauffindbar zu machen. In traditionellen Wissensorganisationssystemen wie Klassifikationen und Thesauri lassen sich mit natürlicher Sprache drei semantische Relationen darstellen: Äquivalenz, Assoziation und Hierarchien. Zwar bietet ein Thesaurus im Vergleich zur einfachen Klassifikation schon vielfältigere Verknüpfungs–möglichkeiten, mit Semantic-Web-Technologien sind jedoch weitaus präzisere Kontextualisierungen möglich. Hier können komplexe Relationen ausgedrückt werden, indem die Objekte beziehungsweise die Ressourcenverbindungen spezifiziert werden. In Beschreibungslogiken wie RDF/RDFS (Resource Description Framework/-Schema ) oder in OWL (Web Ontology Language), lässt sich beispielsweise eine Negation ausdrücken (this property is the inverse of the ‘relatedPartOf’ property, owl:inverseOf ). Über die jeweiligen Daten lassen sich in RDF/RDFs Aussagen treffen, die in sogenannten Tripeln (siehe Abb. 5) modelliert werden. Die einzelnen Tripel werden zu Graphen verbunden. [Fn 40]
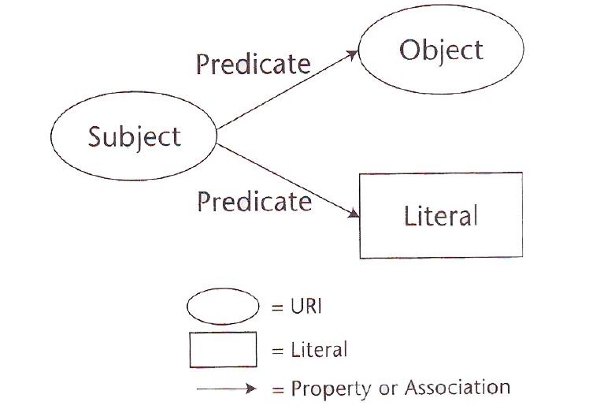
Abbildung 5: RDF Tripel
Durch die Spezifizierung der Verbindung lassen sich konkretere Aussagen treffen, was vor dem Hintergrund der ‚Entstehung’ von Wissen durch Kontextualisierung interessant ist. [Fn 41] Mit dem Semantic Web wird es möglich Konzepte oder Modelle zu repräsentieren, die oftmals ganz andere semantische und logische Bezüge aufweisen als mit den traditionellen Wissensorganisationsysteme abbildbare Gegenstände oder Dokumente. Der ikonische Charakter der Graphen ermöglicht komplexere Zusammenhänge sichtbar zu machen, wobei hier keine einfache Bildlichkeit gemeint ist, sondern eine operationale Ikonizität, da die Bildlichkeit der Tripel durch ihre vorgegebene Dreierstruktur immanent ist. Wie in den EG von Peirce spielt die räumliche Vorstellung eine Rolle: „Räumliche“ Relationen werden zur Darstellung auch nichträumlicher Sachverhalte genutzt. [Fn 42] Die Tripel werden sozusagen auf dem Behauptungsblatt – also im Diskursuniversum – des WWW modelliert. Mit diagrammatischen Mitteln lassen sich, bei allen Beschränkungen, denen sie natürlich auch unterliegen, [Fn 43] komplexere Sachverhalte darstellen. Die Verbindung ikonischer und symbolischer Elemente und die geregelten Transformationsprozeduren bilden einen entscheidenden Vorteil. [Fn 44] Das in der Computerlinguistik formulierte Vorhaben „translating language to logic“ [Fn 45] könnte man daher in diesem Kontext mit dem Zusatz …into iconic logic erweitern. Sicher kann man nicht dafür plädieren, die gesamte Wissensorganisation auf rein bildhafte Systeme umzustellen. Auch diese haben ihre Grenzen und nicht zuletzt der Elaborationsgrad und die Tradierung anderer Verfahren dürften hier Akzeptanzprobleme aufwerfen. Als Ergänzung und Erweiterung bestehender Systeme der Wissensorganisationen bieten sie sich dagegen ausgezeichnet an.
Nicht nur das starke Aufkommen und die hohe Relevanz digitaler Informationen, sondern auch die technischen Möglichkeiten für die Gestaltung von Repräsentationsprozessen haben den Bereich der Wissensorganisation bereits jetzt nachhaltig verändert. [Fn 46] Die Darstellungsmöglichkeiten „operationaler Bildlichkeit“ [Fn 47] finden bereits teilweise praktische Anwendung in den erwähnten Gebieten (conceptual graphs, Semantic Web Technologien). Die Einbeziehung diagrammatischer Ansätze in die theoretische Reflexionsarbeit der Informationswissenschaft, könnte, bei allen terminologischen Übersetzungsproblemen, einen tragfähigen konzeptionellen Rahmen bieten, um neue Formen der Wissensorganisation zu entwickeln.
Fußnoten
[01] Platon, Menon, 80e-d. [zurück]
[02] Cf. Hoffmann (2000). [zurück]
[03] Cf. Gehring et al. (1992), 7. Bei Platon erfüllt die Darstellung eine rein didaktische Funktion (im Auftrag der anamnesis), da im Sinne der platonischen „Ideenlehre“, „Urbilder“ niemals durch „Abbilder“ erreicht werden können. Die Darstellung würde nur von der Wahrheit ablenken. Der Zusammenhang von Signifikant und Signifikat kann aus dieser Perspektive nur als unwesentlich verstanden werden; daher auch das problematische Verhältnis von (empirischer) „Wahrnehmung“ und (wahrem) „Wissen“ im Platonismus. [zurück]
[04] Peirce (1906), 314: „all necessary reasoning is diagrammatic; and the assurance fumished by all other reasoning must be based on necessary reasoning. In this Sense, all reasoning depends directly or indirectly upon diagrams.“ [zurück]
[05] Der Peirce-Spezialist Helmut Pape spricht deshalb auch bei der besonderen Verfahrensweise des Peirceschen Denkens vom Prinzip einer „formativen Visualität“. Cf. Pape (2012). [zurück]
[06] Wobei Kant zwischen erlaubter Analogie und unerlaubten Rückschluss auf das Objekt unterscheidet. Das Kapitel über den „Schematismus des reinen Verstandes“ gilt als recht schwierig und Kant räumt selbst ein, dass der synthetische Vorgang im Dunkeln bleibt. Kant (1998), B 176-187. [zurück]
[07] Gegen Kants Annahme der „synthetischen Urteile a priori“ in der Geometrie erhob allerdings bereits Salomon Maimon Einspruch. Cf. Freudenthal (2012). [zurück]
[08] Peirce legte Wert auf diese Schreibweise, um die Verbindung zu den symptomatologischen Lehren der antiken Medizin zu verdeutlichen. Cf. Krois (2012), 56-59. [zurück]
[09] Wir beziehen uns hier auf die Definitionen, die Peirce im Zusammenhang mit seiner „Spekulativen Grammatik“ formuliert hat, wie sie von Helmut Pape in dem Band Phänomen und Logik der Zeichen auf Deutsch herausgegeben wurde. Selbst dort finden sich alternative Formulierungen, genauso wie in anderen Entwürfen. Diese Unabgeschlossenheit ist einer der Gründe, der die Rezeption von Peirce so schwierig machte. Trotzdem gibt es bei den Definitionen verbindende Merkmale, die auf Peirces drei Grundkategorien von Erstheit, Zweitheit und Drittheit zurückgeführt werden können. Eines dieser Merkmale ist, dass das Verhältnis von Ikon (als „Erstheit“), Index (als „Zweitheit“) und Symbol (als Drittheit“ oder Vermittlung) aufsteigend inklusiv ist. Die Zeichentriade der Z/I-Relation teilt Peirce in: Sumizeichen, Dicizeichen (informative Zeichen) und Suadizeichen (Argumente). Zum Dicizeichen und dem Peirceschen Begriff der Information cf. Stjernfelt (2012), 95-113 insbesondere 96-98. [zurück]
[10] Cf. CP, 2.299. [zurück]
[11] Stjernfelts Diagrammatology (2007) will die Disqu-alifizierung der „Ähnlichkeit“ bzw. der „Ikonizität“ (wie sie z.B. bei Nelson Goodman und – dem frühen – Umberto Eco, wie auch bei französischen strukturalistischen und post-strukturalistischen Theoretikern vorkommt), in Bezug auf die Semiotik und im Sinne eines „semiotic realism“ aufheben. Cf. Stjernfelt (2007), insbesondere: 51-72. [zurück]
[12] CP, 2.279. [zurück]
[13] Peirce (1903), 44. Für eine deutsche Übersetzung und eine alternative Version (Bilder, Diagramme, Metaphern) cf. Papes Edition des „Syllabus“ in: Peirce (1983), 64-65. [zurück]
[14] Die notwendige Strukturähnlichkeit wird durch eine bestimmte Art von Abstraktionen erreicht. Diesen Vorgang nennt Peirce prescission (CP 4.235). Cf. Stjernfelt (2011b). [zurück]
[15] Peirce (1906), 318: ,It is […] a very extraordinary feature of diagrams that they show - as literally show as a percept shows the perceptuai judgement to be true -, that a consequence does follow, and more marvelious yet, that it would follow under all varieties of circumstances accompanying the premisses. It is not, however, the statical Diagram-icon that directly shows this; but the Diagram-icon having been constructed with an Intention, involving a Symbol […], in the light of this intention determines an initial symbolic interpretant. Meanwhile the diagram remains in the field of perception or Imagination; and so the iconic diagram and its initial symbolic interpretant taken together constitute what we shall not too much wrench Kant’s term in calling a Schema, which is on the one side an object capable of being observed while on the other side it is general.“ [zurück]
[16] Cf. Hoffmann (2005), 187-215. [zurück]
[17] CP 8.183, cf. Hoffmann (2005), 38. [zurück]
[18] Cf. Hoffmann (2005), 124. [zurück]
[19] Sprich: genauso präzise ist, aber dafür den entscheidenden Vorteil der Anschaulichkeit bietet. [zurück]
[20] Stjernfelt (2006), 71-72; cf. Stjernfelt (2007), 90. [zurück]
[21] Cf. Stjernfelt (2006) und Stjernfelt (2011a). [zurück]
[22] CP, 4.432. [zurück]
[23] Ziel sei es dabei, so Stjernfelt, „[to] depict logical relations like they really are, thus adding to the pragmatist operational criterion of iconicity an ontologically motivated extra criterion. According to this criterion, if two icons are equivalent according to [operational] iconicity (1), still the representation which is most iconical according to [optimal] iconicity (2) must be preferred – if heuristic arguments do not count against it, that is.” Stjernfelt (2006), 77. [zurück]
[24] CP, 4.561, Fn. 1. [zurück]
[25] Ebd. [zurück]
[26] Cf. Shins Eintrag „Diagrams“ in der Stanford Encyclopedia of Philosophy, online unter: http://plato.stanford.edu/entries/diagrams. [zurück]
[27] Shin 2011. [zurück]
[28] Ebd., 45-46. [zurück]
[29] Siehe dazu Abbildung 2 (rechte Spalte). [zurück]
[30] Für einen Beweis cf. Shin 2002, § 4.2.2. [zurück]
[31] Pape (2012), 69. [zurück]
[32] Cf. Peirce (1983), 143 ff. [zurück]
[33] Wobei es bei den Gammagraphen auch diskontinuierliche cuts geben kann (heißt dann: ‚möglicherweise nicht‘). [zurück]
[34] Mit herzlichem Dank an Franz Engel für die Bilder. [zurück]
[35] Zur genauen Unterscheidung von EG und CG cf. John F. Sowa (1997): Peircean Foundations for a Theory of Context, 10. [zurück]
[36] Dazu u.a. LIBREAS. Library Ideas 15 (2009): A Semiotic Turn? & Open Access und Geisteswissenschaften. [zurück]
[37] Cf. Brier (2008). [zurück]
[38] So wie es Mehler (2011) für den Interaktivitätsbegriff vornimmt. [zurück]
[39] Brier (2008), 289. [zurück]
[40] Cf. Palmer, Sean B. (2001): The Semantic Web: An Introduction. Online: http://infomesh.net/2001/swintro/. [zurück]
[41] Diese Auffassung des Wissensbegriffs beruht unter anderem auf dem DIKW-Modell von Jennifer Rowley, (2007): „The wisdom hierarchy. Representations of the DIKW hierarchy” in: Journal of Information Science, 33 (2), 163-180. Siehe auch ‚Unaggregated data […] have no meaning in themselves, Gradmann, Stefan (2010): Knowledge = Information in Context, 3. [zurück]
[42] Somit ist die diagrammatische Repräsentation auch in der Lage verschiedene Dimensionen der Raumzeit darzustellen. Cf. Wilharm (1992), 127; sowie: May & Stjernfelt (2008). [zurück]
[43] Cf. Shin (1994). [zurück]
[44] Diese These weist Heiner Wilharm überzeugend nach in ‚Ein Bild sagt mehr als tausend Worte. Über Begriff und Verwendung diagrammatischer Darstellungen in Philosophie und Wissenschaft.’ (1992), 121-160. [zurück]
[45] John F. Sowa (1997), o.S. [zurück]
[46] Sutter & Mehler (2010), 7: „ Die Herausforderung, die der Wandel von Kommunikationsmedien […] darstellt, resultiert nicht nur aus der ungeheuren Beschleunigung des Medienwandels. Die Herausforderung stellt sich auch mit Frage, welches die neuen Formen und Strukturen sind, die aus dem Wandel der Medien hervorgehen.“ [zurück]
[47] Cf. Krämer (2009). [zurück]
Bildnachweise
Abb 1: Salomonsson, B. (2008): http://www.pep-web.org/document.php?id=anijp-de.003.0221a.
Abb 2: Peirce, Charles S. (1993): Phänomen und Logik der Zeichen. Hrsg. und übers. von Helmut Pape, 2. Aufl. Frankfurt am Main : Suhrkamp, 172.
Abb. 3 und 4: Engel, Franz: „Epistêmy und andere Grotesken“ in Engel, Franz; Queisner, Moritz; Viola, Tullio (Hg.) (2012): Das bilderische Denken von Charles S. Peirce. Berlin : Akademie Verlag, 156 u. 157.
Abb. 5: The RDF triple: Michael C. Daconta (2003): The Semantic Web. A Guide to the Future of XML, Web Services and Knowledge Management, 88.
Literatur
Brier, Søren (2008): Cybersemiotics. Why Information Is Not Enough! Toronto Studies in Semiotics and Communication. Toronto : Univ. of Toronto Press.
Engel, Franz; Queisner, Moritz; Viola, Tullio (Hg.): Das bilderische Denken: Charles S. Peirce. Berlin : Akademie Verlag. 2012.
Freudenthal, Gideon (2012): „Anschauung und Verstand in geometrischen Konstruktionen: Kant und Maimon“ in: Dietzsch, Steffen; Tietz, Udo (Hg.): Transzendentalphilosophie und die Kultur der Gegenwart. Leipzig : Universitätsverlag, 113-138. (im Erscheinen)
Friedman, Alon; Thellefsen, Martin (2011): „Concept theory and semiotics in knowledge organization” in: Journal of Documentation, Vol. 67, No 4, 644-674, DOI: http://dx.doi.org/10.1108/00220411111145034.
Gehring, Petra et al. (1992): Diagrammatik und Philosophie. Amsterdam [u.a.] : Rodopi.
Glasgow, Janice et al. (Hg. (1995). Diagrammatic Reasoning. Cognitive and Computational Perspectives. Menlo Park CA : AAAI Press and MIT-Press.
Gradmann, Stefan (2010): Knowledge = Information in Context. On the Importance of Semantic Contextualisation in Europeana, Europeana White Paper No. 1, S.4. Online: http://www.scribd.com/doc/32110457/Europeana-White-Paper-1.Gradmann.
Hoffman, Michael H. G. (2000): „Die Paradoxie des Lernens und ein semiotischer Ansatz zu ihrer Auflösung“ in: Zeitschrift für Semiotik 22/1, 31-50.
Hoffman, Michael H. G. (2005): Erkenntnisentwicklung. Ein semiotisch-pragmatischer Ansatz. Frankfurt am Main : Klostermann
Kant, Immanuel (1781/1787): Kritik der reinen Vernunft. Hamburg : Meiner, 1998
Krämer, Sybille (2009): „Operative Bildlichkeit. Von der ‚Grammatologie’ zu einer ‚Diagrammatologie’? Reflexionen über erkennendes Sehen“ in: Heßler, Martina; Mersch, Dieter: Logik des Bildlichen. Zur Kritik der ikonischen Vernunft. Bielefeld : transcript, 2009, 94-122.
Krois, John Michael (2012): „Eine Tatsache und zehn Thesen zu Peirce‘ Bildern“ in: Engel et al. (Hg.): Das bildnerische Denken: Charles S. Peirce. Berlin : Akademie Verlag. 53-64.
LIBREAS. Library Ideas 15 (2009): A Semiotic Turn? & Open Access und Geisteswissenschaften.
May, Michael (1995): „Diagrammatisches Denken. Zur Deutung logischer Diagramme als Vorstellungsschemata bei Lakoff und Peirce“ in: Zeitschrift für Semiotik 17/3-4, 285-305.
May, Michael; Stjernfelt, Frederik (2008): „Measurement, Diagram, Art. Reflections on the role of the icon in science and aesthetics“ in: Søndergaard, Morten; Weibel, Peter (Hg.): Magnet. Thorbjørn Lausten‘s Visual Systems. Heidelberg : Kehrer Verlag 2008, 53-73. Online: http://www.academia.edu/1272790/Measurement_Diagram_Art_2008_.
Mehler, Alexander (2011): „Artifizielle Interaktivität. Eine semiotische Betrachtung“ in: Sutter, Tilmann; Mehler, Alexander (Hg.): Medienwandel als Wandel von Interaktionsformen. Wiesbaden : VS Verlag, 107-134.
Palmer, Sean B. (2001): The Semantic Web: An Introduction. Online: http://infomesh.net/2001/swintro/.
Pape, Helmut (2012): „Was ist Peirce‘ bildnerisches Denken?“ in: Engel et al. (Hg.): Das bildnerische Denken: Charles S. Peirce. Berlin : Akademie Verlag.65-92.
Peirce, Charles S. (1903): „A Syllabus“ (MS 478)
Peirce, Charles S. (1906): „Prolegomena for an Apology for Pragmatism“ in: Carolyn Eisele (Hg.), The New Elements of Mathemalics. Bd. IV. Den Haag: Mouton, 1976, 313-330.
Peirce, Charles S. (1931-1958): Collected Papers of Charles Sanders Peirce (CP), 8 Bd., hg. v. Hartsthorne, Weiss & Burks, Cambridge, MA : Harvard University Press.
Peirce, Charles S. (1983): Phänomen und Logik der Zeichen. Hg. und übers. von Helmut Pape, Frankfurt am Main : Suhrkamp.
Platon (1993): Menon. Hamburg : Meiner.
Rowley, Jennifer (2007): „The wisdom hierarchy. Representations of the DIKW hierarchy” in: Journal of Information Science, 33 (2), 163-180.
Shin, Sun Joo (1994): The Logical Status of Diagrams. Cambridge / New York: Cambridge University Press.
Shin, Sun Joo (1999): „Reconstituting Beta Graphs into an Efficacious System“, Journal of Logic, Language and Information archive, 8/3, 273-295.
Shin, Sun Joo (2002): The iconic logic of Peirce’s graphs, Cambridge, MA: MIT Press
Shin, Sun Joo (2011): „Existential Graphs as Efficient, Formal, Representation System for Logic“ in: Cybernetics and Human Knowing 18/1-2, 29-47.
Sowa, John F. (1997): „Peircean Foundations for a Theory of Context“ in: Conceptual Structures. Fulfilling Peirce’s Dream. Lecture Notes in Computer Science, Volume 1257/1997, 41-64, Online: http://users.bestweb.net/~sowa/ontology/contexts.htm.
Stjernfelt, Frederik (2006): „Two Iconicity Notions in Peirce’s Diagrammatology“ in: Conceptual Structures. Inspiration and Application. Berlin, Heidelberg : Springer, 70-86 (Lecture Notes in Artificial Intelligence , Vol. 4068)
Stjernfelt, Frederik (2007): Diagrammatology. Berlin, Heidelberg : Springer.
Stjernfelt, Frederik (2011a) „On operational and optimal iconicity in Peirce’s diagrammatology“ in: Semiotica 186–1/4 (2011), 395–419.
Stjernfelt, Frederik (2011b): Peirce’s Notion of Diagram Experiment: Corollarial and Theorematical Experiments with Diagrams. In: Heinrich et al (Hg.) Image and Imaging in Philosophy, Science and the Arts. Bd. 2, Ontos Verlag. 305-340.
Sutter, Tilmann; Mehler, Alexander (2011): „Einleitung: Der aktuelle Medienwandel im Blick einer interdisziplinären Medienwissenschaft“ in: Dies. (Hg.): Medienwandel als Wandel von Interaktionsformen. Wiesbaden : VS Verlag, 7-16.
Wilharm, Heiner (1992): „Ein Bild sagt mehr als Tausend Worte. Über Begriff und Verwendung diagrammatischer Darstellungen in Philosophie und Wissenschaft“ in: Gehring, Petra et al. (Hg.): Diagrammatik und Philosophie, 121-160.
Linda Treude (M.A) studierte Bibliotheks- und Informationswissenschaft sowie Kunstgeschichte an der Humboldt-Universität zu Berlin. Sie promoviert zum Thema Schrift und Bild, speziell zur Darstellbarkeit logischer und semantischer Relationen in digitalen Netzen. Seit 2011 ist sie Projektmitarbeiterin beim Computer- und Medienservice der HU.
Sascha Freyberg (M.A.) studierte Kulturwissenschaften und Philosophie in Hagen und Berlin,arbeitete am Max-Planck-Institut für Wissenschaftsgeschichte und ist derzeit mit der wissenschaftlichen Erschliessung eines Nachlasses an der Kolleg-Forschergruppe Bildakt und Verkörperung an der HU beschäftigt.
